by
Robin Wilson, Penguin 2002
I liked this book better than Singh's on
Fermat's Last Theorem. Singh, as I recall, spends a lot of time on familiar basics (what is a prime, what is a Diophantine equation) and then -- blammo -- modular elliptic forms. The four-color map problem, at 150 years, is only half as old as Fermat's, but the details are much less familiar, and the steps of the proof are almost easy to follow, at least as presented here.
For example, we can limit consideration to maps with only three lines meeting at each vertex ("cubic maps"). If you have more, stick a small patch over the vertex, and any coloring that works on this new map will work when the patch is reduced to a point. Once you consider a cubic map, you can use Euler's formula F - E + V = 2 to show that every such map has at least one country with five or fewer neighbors. This is an example of an "unavoidable set". (By the way, I remember reading in college a lovely lucid book on the nature of proof, that uses Euler's formula as its basic example. The title is
Proofs and Refutations
by Imre Lakatos ). In turn, you can directly use the 5-neighbor result to prove that six colors suffice. It is also clearly explained how a minimal uncolorable map cannot have a digon, triangle, or square in it. (The key notion here is "reducibility" -- showing that a minimal uncolorable map can be made smaller, proving by contradiction). The case of a pentagon is harder to prove, and led to the Kempe-chain argument, which brings up another fun feature of the book: a lot of people got a lot of things wrong. Kempe's proof was accepted for 11 years, until it was found to have a problem. Another mathematician proposed that all cubic polyhedra have a Hamiltonian cycle, but 65 years later Bill Tutte discovered one that does not (see picture).
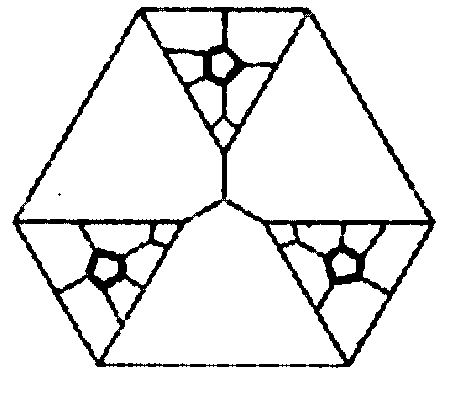
And that's another point in the book's favor, at least for me. It adds to my list of mathematical quilt patterns that Patricia will have to do someday. Here is a fine quilt design that shows a necessary 12-coloring for the "empire problem" where each empire (which must be colored the same) has only two countries:
There must be a drawing program in which one could straighten the edges.
The book is certainly written by an academic, you can tell by the lame jokes (an "apple" pun on Appel's name). But some things are funny: one mathematician's wife asking another if she also had spent her honeymoon coloring in maps. And the research seems thorough. The biblio shows several other books on the topic -- I don't know what they are like. Many people felt the pull of the problem: the French poet Paul Valery, for example. Minkowski dismissed the problem as unworked-on by good mathematicians, but admitted hubris after an intense few weeks looking at it.
And that of course brings us to the central point of interest: that the proof was computer-aided in a big way. It took over 1000 hours to check an unavoidable set of 1936 reducible configurations. This was preceded by a classic screw-up where someone hacked a program to ignore some configurations that were too hard to check, someone else used the results without noting the hack, and a false proof that was detected only with difficulty. Then hardware mavens told Haaken he would have to wait a couple of years for faster computers, but young Appel said that it was just a matter of better programming (how familiar this all is). H&A attribute their earlier success to focusing on doing the unavoidable-check first, while others focused on reducibility. The proof's reception was cold, and split this way: the older mathematicians refused to believe a proof done by computer, and the younger ones refused to believe that the associated 700 hand-done calculations could be without flaw. Ian Stewart summarises the most common complaint:
The answer appears as a kind of monstrous coincidence. Why is there an unavoidable set of reducible configurations? The best answer at the present time is: there just is. The proof: here it is, see for yourself. The mathematician's search for hidden structure, his pattern-binding urge, is frustrated.
This was in 1976 (my fellow geeks will remember the excitement in Scientific American). Since then, the proof has been tested, for example with a similar proof involving just 633 configurations (and probably a lot less computer time) in 1994. In fact, you can get the source code here and check it yourself in 3 hours. But there is no "elegant" proof (though there are some cool results for surfaces with holes). Do you think there will be?
Sundry sites: MathWorld Ivars Peterson Related fiction
John wrote: one of your best
Madeleine wrote: I don't have the faintest clue what you're talking about, except the part where you expect Patricia to make a quilt from one of these proofs which no doubt will take the better part of her life